Oranlı ve Oransız Sayılar

[eLanuR]

Oranlı (Rasyonel) sayılar

Matematikte, rasyonel veya oranlı sayılar (veya kesirler) iki tamsayının birbirine oranı ile ifade edilebilen sayılardır. Oranlı sayılar b sıfır olmamak üzere a/b şeklinde (a ve b tamsayı) yazılabilir. 2/3 ve 4/6 veya 6/9 eşdeğer oranlı sayılardır. Dolayısıyla her oranlı sayı sonsuz şekilde ifade edilebilir. Oranlı sayıların en basit formu a ve b tamsayılarının ortak böleninin olmadığı a/b ifadesidir.


Her tam sayı oranlı sayıdır. Çünkü v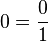eya veya şeklinde yani oranlı sayı tanımına uygun biçimde yazılabilirler. Oranlı sayılar kümesi, tam sayılar kümesi 'yi kapsar. Yani .


Tanım

Oranlı sayılar kümesi, tam sayıların bir genişlemesidir ve Q ile veya ile gösterilir. kümesi genelde şöyle tanımlanır:



Daha ince bir tanımı ise tam sayılar üzerinden tanımlanacak bir denklik bağıntısıyla yapılabilir. Böylece her denklik sınıfı bir oranlı sayı olarak anılır. kümesinden seçilmiş keyfî (a,b) ve (c,d) öğeleri için "~" bağıntısı




olarak tanımlansın. Bunun bir denklik bağıntısı olduğu kolaylıkla kanıtlanabilir. Bu durumda, denklik sınıfları



olurlar. Oranlı sayı ise basitçe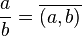



şeklinde tanımlanır.
Tanımda paydanın sıfır olmama şartı ifadesinin tanımlanmamış olmasındandır. Bir sayının sıfıra bölümü tanımsızdır.

Oransız (irrasyonel) sayılar

Oransız sayılar (ya da İrrasyonel sayılar), rasyonel sayılar kümesine dahil olmayan reel sayılardır. Kesir olarak ifade edilemeyen bu sayılara π, e ve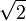

Örnekler: 3√7, √2, 5√(9/8)...

3√64 veya √(4/9) irrasyonel sayılar değildir çünkü rasyonel karşılıkları vardır:

3√64=4

√(4/9)=2/3
örnek verilebilir. Q' veya I ile gösterilir. Bu sayılar belli bir düzeni olmaksızın sonsuza kadar devam eden ondalık sayılar (örneğin pi sayısı) veya rasyonel karşılığı olmayan kökler olabilir.