|
|
#1
9 December 2008, 15:05
|
|||
|
|||
Fermat'nın Son Teoremi
Fermat'nın Son Teoremi
Fransız matematikçi [Link'i Görebilmeniz İçin Kayıt Olunuz.! Kayıt OL]'nın 17. yüzyılda öne sürdüğü fakat kanıtı ancak 1994 yılında İngiliz matematikçi [Link'i Görebilmeniz İçin Kayıt Olunuz.! Kayıt OL] tarafından verilen teoremdir. İfadesinin ortaokul matematik bilgileriyle anlaşılacak kadar yalın olmasına karşılık öne sürülmesiyle kanıtlanması arasında geçen çok uzun sürede pek çok ünlü matematikçi tarafından üzerinde uğraşılıp da kanıtlanamamış olmasıyla matematik tarihinde öne çıkmıştır. Kısaca, eğer n ikiden büyük bir tamsayıysa, ve x, y, z sayıları pozitif tamsayılar ise 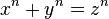 ifadesinin sağlanamayacağını ifade eder. İfadenin n=1 ve n=2 durumlarında kolayca sağlanabileceğini görmek zor değildir. Biraz açmak gerekirse, n=2 durumu ünlü [Link'i Görebilmeniz İçin Kayıt Olunuz.! Kayıt OL] 'nin bizzat kendisidir. x=3, y=4, z=5 veya x=5, y=12, z=13 tamsayı üçlüleriyle kolayca sağlanır.Bu sanının (artık teorem demek gerekiyor elbette) kanıtı için pek çok matematikçi uğraşmış ancak başarısız olmuşlardır. Ancak yakın tarihlere kadar çok büyük n değerleri için bu sanının doğrulanmasına devam edilmiştir. Bu tür kısmi ilerlemelere yönelik çabalar, hiç beklenmedik bir zamanda İngiliz matematikçi Andrew Wiles'ın bir kanıt bulduğunu duyurmasıyla son bulmuştur. Ne var ki kısa sürede Andrew Wiles'ın kanıtında bir hata bulunmuş ve Andrew Wiles uzun ve yorucu bir çabanın sonunda 1994 yılında uzmanlarca doğruluğu kabul gören bir kanıt vermeyi başarmıştır. Aslında Wiles'ın kanıtı [Link'i Görebilmeniz İçin Kayıt Olunuz.! Kayıt OL]'nın son teoreminden daha güçlü bir ifadenin, [Link'i Görebilmeniz İçin Kayıt Olunuz.! Kayıt OL]'nün de doğruluğunu göstermiştir. Söz konusu kanıt [Link'i Görebilmeniz İçin Kayıt Olunuz.! Kayıt OL]'nin çok gelişkin tekniklerini kullanır. 
|
Normal
