|
|
#1
9 December 2008, 15:12
|
|||
|
|||
Limit
Limit Limit kelimesi Latince Limes ya da Limites 'den gelmekte olup sınır, uç nokta anlamdadır. Öklid ve Arşimet tarafından eğrisel kenarlara sahip şekillerle ilgili olan teoremlerde kullanılmıştır. Limit kavramı, çok önceleri kullanılmasına rağmen sonra unutulmuş ve daha sonra Newton ile Leibniz'in eserlerinde görülmüştür. Mesela, diferansiyel hesapta bir eğri (daire gibi) sonsuz küçük uzunlukta sonsuz kenara sahip bir çokgen olarak kabul edilir. Limit kavramından ortaya çıkan diferansiyel hesap, pekçok fizik probleminin kolayca ele alınmasına sebep oluyor. Matematiksel kullanımı f(x) fonksiyonu bir açık aralıkta tanımlanmış olsun, ve L bir gerçel sayı olsun. 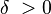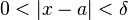Bütün  değerleri için, bir  bulunabiliyor, öyle ki bütün  sağlayan x için ,  eşitsizliği doğru ise; L, f(x)'in a noktasındaki limitidir.Bir fonksiyonun a'daki limiti (L):  şeklinde gösterilir.Önemli limitler BİR FONKSİYONUN LİMİTİ
TANIM A R ve f: A – {xo} R ‘ye bir fonksiyon F(x) olsun. x değişkeni xoR sayısına yaklaştığında f(x) fonksiyonu da tR’ye yaklaşıyorsa t gerçel sayısına x, xo’a yaklaşırken f(x) fonksiyonunun limiti denir ve lim f(x) = t xxo şeklinde gösterilir. SAĞDAN VE SOLDAN LİMİT: SAĞDAN LİMİT: y = f(x) fonksiyonunda x, xo R değerine sağ taraftan yaklaşırken f de bir t1 R değerine yaklaşıyorsa t1’e fonksiyonun sağdan limiti denir ve lim f(x) = t1 biçiminde x x+o gösterilir. SOLDAN LİMİT: y = f(x) fonksiyonunda x, xo R değerine sol taraftan yaklaşırken f de bir t2 R değerine yaklaşıyorsa t2 ye fonksiyonun soldan limiti denir ve lim f(x) = t2 xx-o 
|
Normal
